How to Estimation Continuous Time Stochastic Processes

Continuous-time Processes¶

The stochastic.processes.continuous module provides classes for generating discretely sampled continuous-time stochastic processes.

stochastic.processes.continuous.BesselProcess
stochastic.processes.continuous.BrownianBridge
stochastic.processes.continuous.BrownianExcursion
stochastic.processes.continuous.BrownianMeander
stochastic.processes.continuous.BrownianMotion
stochastic.processes.continuous.CauchyProcess
stochastic.processes.continuous.FractionalBrownianMotion
stochastic.processes.continuous.GammaProcess
stochastic.processes.continuous.GeometricBrownianMotion
stochastic.processes.continuous.InverseGaussianProcess
stochastic.processes.continuous.MixedPoissonProcess
stochastic.processes.continuous.MultifractionalBrownianMotion
stochastic.processes.continuous.PoissonProcess
stochastic.processes.continuous.SquaredBesselProcess
stochastic.processes.continuous.VarianceGammaProcess
stochastic.processes.continuous.WienerProcess

class stochastic.processes.continuous. BesselProcess ( dim=1, t=1, rng=None ) [source]¶

Bessel process.

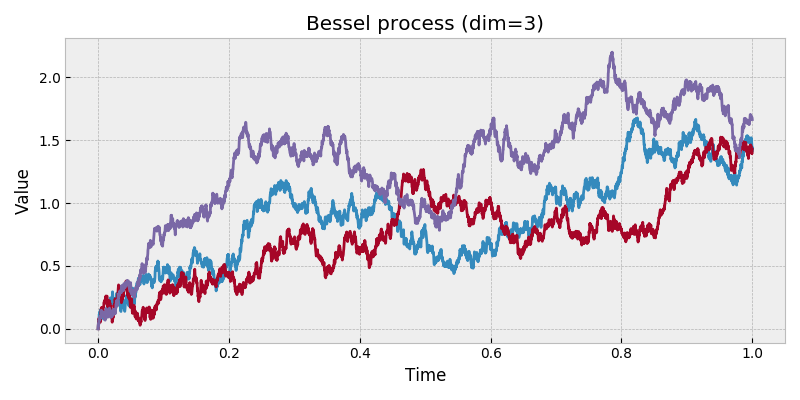
The Bessel process is the Euclidean norm of an $n$-dimensional Wiener process, e.g. $\|\mathbf{W}_t\|$

Generate Bessel process realizations using dim independent Brownian motion processes on the interval $[0,t]$

Parameters

dim (int) – the number of underlying independent Brownian motions to use
t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

sample ( n ) [source]¶

Generate a realization.

Parameters: n (int) – the number of increments to generate

sample_at ( times ) [source]¶

Generate a realization using specified times.

Parameters: times – a vector of increasing time values at which to generate the realization

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

class stochastic.processes.continuous. BrownianBridge ( b=0, t=1, rng=None ) [source]¶

Brownian bridge.

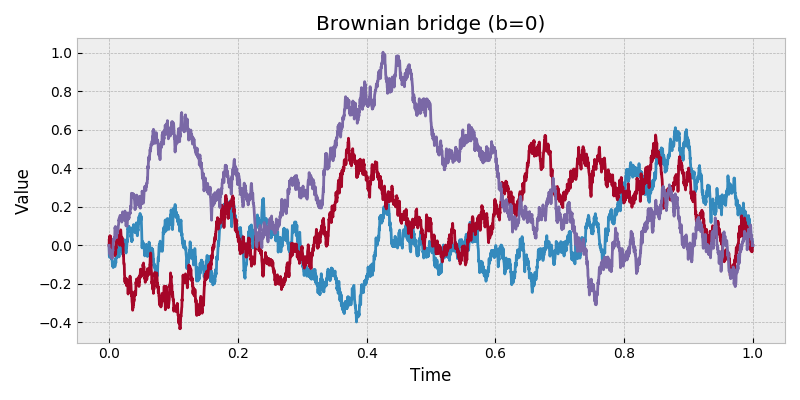
A Brownian bridge is a Brownian motion with a conditional value on the right endpoint of the process.

Parameters

b (float) – the right endpoint value of the Brownian bridge at time t
t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

property b¶: Right endpoint value.

sample ( n ) [source]¶

Generate a realization.

Parameters: n (int) – the number of increments to generate

sample_at ( times, b=None ) [source]¶

Generate a realization using specified times.

Parameters

times – a vector of increasing time values at which to generate the realization
b (float) – the right endpoint value for times [-1]

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

class stochastic.processes.continuous. BrownianExcursion ( t=1, rng=None ) [source]¶

Brownian excursion.

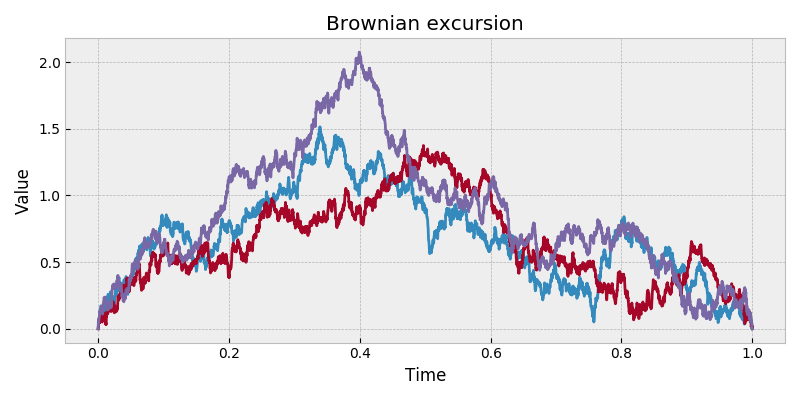
A Brownian excursion is a Brownian bridge from (0, 0) to (t, 0) which is conditioned to be nonnegative on the interval [0, t].

Generated using method by

Biane, Philippe. "Relations entre pont et excursion du mouvement Brownien reel." Ann. Inst. Henri Poincare 22, no. 1 (1986): 1-7.
Vervaat, Wim. "A relation between Brownian bridge and Brownian excursion." The Annals of Probability (1979): 143-149.

Parameters

t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

sample ( n ) [source]¶

Generate a realization.

Parameters: n (int) – the number of increments to generate.

sample_at ( times ) [source]¶

Generate a realization using specified times.

Parameters: times – a vector of increasing time values at which to generate the realization

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

class stochastic.processes.continuous. BrownianMeander ( t=1, rng=None ) [source]¶

Brownian meander process.

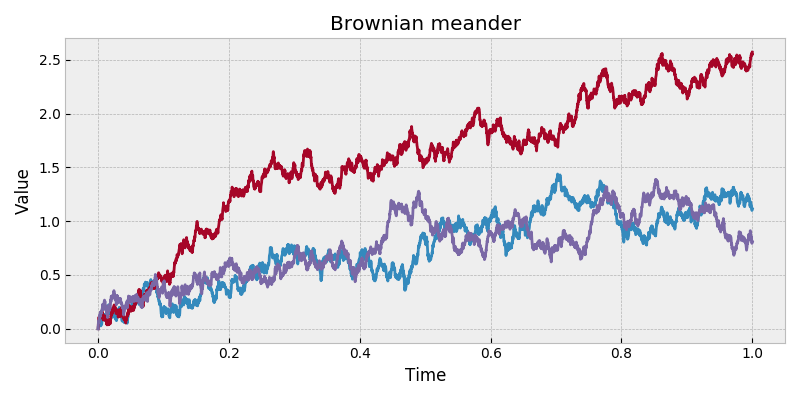
A Brownian motion conditioned such that the process is nonnegative.

Generated using method by

Williams, David. "Decomposing the Brownian path." Bulletin of the American Mathematical Society 76, no. 4 (1970): 871-873.
Imhof, J-P. "Density factorizations for Brownian motion, meander and the three-dimensional Bessel process, and applications." Journal of Applied Probability 21, no. 3 (1984): 500-510.

Parameters

t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

sample ( n, b=None ) [source]¶

Generate a realization.

Parameters

n (int) – the number of increments to generate
b (float) – the nonnegative right hand endpoint of the meander. If not provided, one is randomly selected from a $\sqrt{2E}$ random variable where $E$ is exponential.

sample_at ( times, b=None ) [source]¶

Generate a realization using specified times.

Parameters

times – a vector of increasing time values at which to generate the realization
b (float) – the right endpoint value for times [-1]. If not provided, one is randomly selected from a $\sqrt{2tE}$ random variable where $E$ is exponential and $t$ is times [-1].

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

class stochastic.processes.continuous. BrownianMotion ( drift=0, scale=1, t=1, rng=None ) [source]¶

Brownian motion.

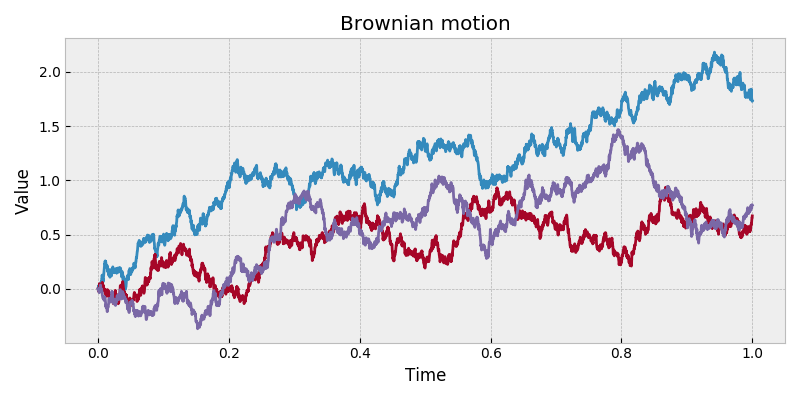
A standard Brownian motion (discretely sampled) has independent and identically distributed Gaussian increments with variance equal to increment length. Non-standard Brownian motion includes a linear drift parameter and scale factor.

Parameters

drift (float) – rate of change of the expected value
scale (float) – scale factor of the Gaussian process
t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

property drift¶: Drift parameter.

sample ( n ) [source]¶

Generate a realization.

Parameters: n (int) – the number of increments to generate

sample_at ( times ) [source]¶

Generate a realization using specified times.

Parameters: times – a vector of increasing time values at which to generate the realization

property scale¶: Scale parameter.

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

class stochastic.processes.continuous. CauchyProcess ( t=1, rng=None ) [source]¶

Symmetric Cauchy process.

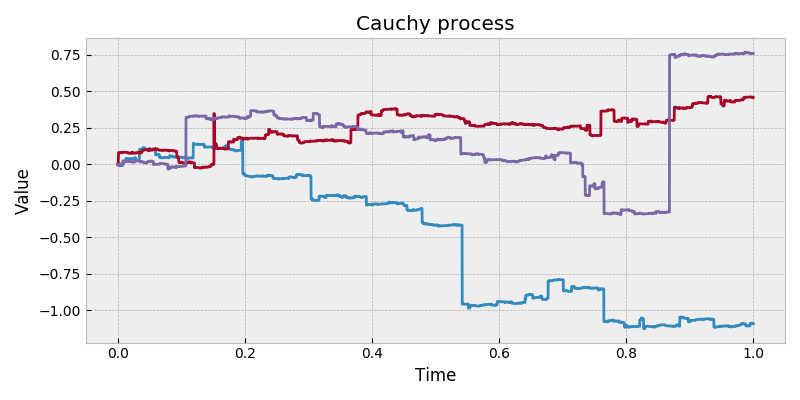
The symmetric Cauchy process is a Brownian motion with a Levy subordinator using location parameter 0 and scale parameter $t^2/2$.

Parameters

t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

sample ( n ) [source]¶

Generate a realization.

Parameters: n (int) – the number of increments to generate.

sample_at ( times ) [source]¶

Generate a realization using specified times.

Parameters: times – a vector of increasing time values at which to generate the realization

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

class stochastic.processes.continuous. FractionalBrownianMotion ( hurst=0.5, t=1, rng=None ) [source]¶

Fractional Brownian motion process.

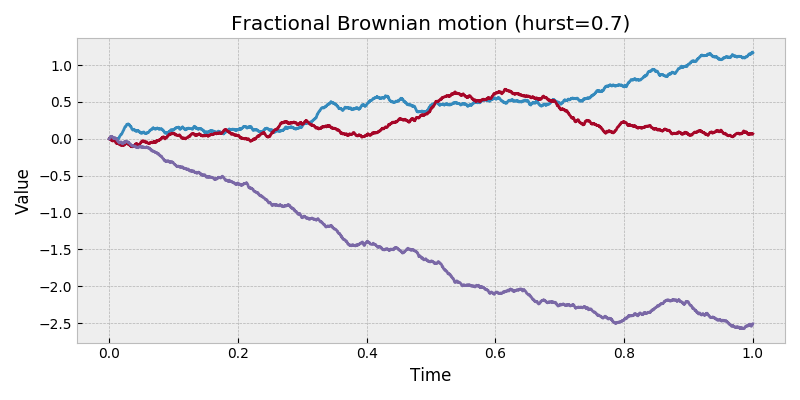
$_images/fractional_brownian_motion.png$

A fractional Brownian motion (discretely sampled) has correlated Gaussian increments defined by Hurst parameter $H$. When $H = 1/2$, the process is a standard Brownian motion. When $H > 1/2$, the increments are positively correlated. When $H < 1/2$, the increments are negatively correlated.

Hosking's method:

Hosking, Jonathan RM. "Modeling persistence in hydrological time series using fractional differencing." Water resources research 20, no. 12 (1984): 1898-1908.

Davies Harte method:

Davies, Robert B., and D. S. Harte. "Tests for Hurst effect." Biometrika 74, no. 1 (1987): 95-101.

Parameters

hurst (float) – the Hurst parameter on the interval (0, 1)
t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

property hurst¶: Hurst parameter.

sample ( n ) [source]¶

Generate a realization.

Parameters: n (int) – the number of increments to generate

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

class stochastic.processes.continuous. GammaProcess ( mean=None, variance=None, rate=None, scale=None, t=1, rng=None ) [source]¶

Gamma process.

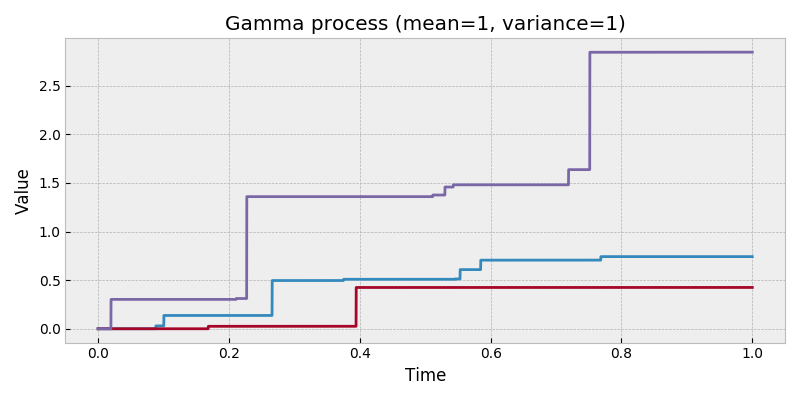
A Gamma process (discretely sampled) is the summation of stationary independent increments which are distributed as gamma random variables. This class supports instantiation using the mean/variance parametrization or the rate/scale parametrization.

Parameters

mean (float) – mean increase per unit time; supply with variance
variance (float) – variance of increase per unit time; supply with mean
rate (float) – the rate of jump arrivals; supply with scale
scale (float) – the size of the jumps; supple with rate
t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

property mean¶: Mean increase per unit time.

property rate¶: Rate of jump arrivals.

sample ( n ) [source]¶

Generate a realization.

Parameters: n (int) – the number of increments to generate

sample_at ( times ) [source]¶

Generate a realization at specified times.

Parameters: times – a vector of increasing time values at which to generate the realization

property scale¶: Scale parameter for jump sizes.

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

property variance¶: Variance of increase per unit time.

class stochastic.processes.continuous. GeometricBrownianMotion ( drift=0, volatility=1, t=1, rng=None ) [source]¶

Geometric Brownian motion process.

A geometric Brownian motion $S_t$ is the analytic solution to the stochastic differential equation with Wiener process $W_t$:

\[dS_t = \mu S_t dt + \sigma S_t dW_t\]

and can be represented with initial value $S_0$ in the form:

\[S_t = S_0 \exp \left( \left( \mu - \frac{\sigma^2}{2} \right) t + \sigma W_t \right)\]

Parameters

drift (float) – the parameter $\mu$
volatility (float) – the parameter $\sigma$
t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

property drift¶: Geometric Brownian motion drift parameter.

sample ( n, initial=1 ) [source]¶

Generate a realization.

Parameters

n (int) – the number of increments to generate.
initial (float) – the initial value of the process $S_0$.

sample_at ( times, initial=1 ) [source]¶

Generate a realization using specified times.

Parameters

times – a vector of increasing time values at which to generate the realization
initial (float) – the initial value of the process $S_0$.

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

property volatility¶: Geometric Brownian motion volatility parameter.

class stochastic.processes.continuous. InverseGaussianProcess ( mean=None, scale=1, t=1, rng=None ) [source]¶

Inverse Gaussian process.

An inverse Gaussian process has independent increments which follow an inverse Gaussian distribution with parameters defined by a monotonically increasing function, $\Gamma(t)$. E.g. for increment $[s, t]$:

$\mathcal{IG}(\Gamma(t) - \Gamma(s), \eta(\Gamma(t) - \Gamma(s))^2)$

Uses a method for generating inverse Gaussian variates from:

Michael, John R., William R. Schucany, and Roy W. Haas. "Generating random variates using transformations with multiple roots." The American Statistician 30, no. 2 (1976): 88-90.

Parameters

mean (callable) – a callable with one argument $\Gamma(t)$ such that $\Gamma(t') > \Gamma(t) \forall t' > t$. Default is the identity function.
scale (float) – scale factor of the shape parameter of the inverse gaussian, or $\eta$ from the above equation.
t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

property mean¶: Mean function.

sample ( n ) [source]¶

Generate a realization.

Parameters: n (int) – the number of increments to generate

sample_at ( times ) [source]¶

Generate a realization using specified times.

Parameters: times – a vector of increasing time values at which to generate the realization

property scale¶: Scale parameter.

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

class stochastic.processes.continuous. MixedPoissonProcess ( rate_func, rate_args=None, rate_kwargs=None, rng=None ) [source]¶

Mixed poisson process.

A mixed poisson process is a Poisson process for which the rate is a scalar random variate. The sample method will generate a random variate for the rate before generating a Poisson process realization with the rate. A Poisson process with rate $\lambda$ is a count of occurrences of i.i.d. exponential random variables with mean $1/\lambda$. Use the rate attribute to get the most recently generated random rate.

Parameters

rate_func (callable) – a callable to generate variates of the random rate
rate_args (tuple) – positional args for rate_func
rate_kwargs (dict) – keyword args for rate_func
rng (numpy.random.Generator) – a custom random number generator

property rate¶

The most recently generated rate.

Attempting to get the rate prior to generating a sample will raise an AttributeError .

property rate_args¶: Positional arguments for the rate function.

property rate_func¶: Current rate's distribution.

property rate_kwargs¶: Keyword arguments for the rate function.

sample ( n=None, length=None ) [source]¶

Generate a realization.

Exactly one of n and length must be provided. Generates a random variate for the rate, then generates a Poisson process realization using this rate.

Parameters

n (int) – the number of arrivals to simulate
length (int) – the length of time to simulate; will generate arrivals until length is met or exceeded.

class stochastic.processes.continuous. MultifractionalBrownianMotion ( hurst=None, t=1, rng=None ) [source]¶

Multifractional Brownian motion process.

$_images/multifractional_brownian_motion.png$

A multifractional Brownian motion generalizes a fractional Brownian motion with a Hurst parameter which is a function of time, $h(t)$. If the Hurst is constant, the process is a fractional Brownian motion. If Hurst is constant equal to 0.5, the process is a Brownian motion.

Approximate method originally proposed for fBm in

Rambaldi, Sandro, and Ombretta Pinazza. "An accurate fractional Brownian motion generator." Physica A: Statistical Mechanics and its Applications 208, no. 1 (1994): 21-30.

Adapted to approximate mBm in

Muniandy, S. V., and S. C. Lim. "Modeling of locally self-similar processes using multifractional Brownian motion of Riemann-Liouville type." Physical Review E 63, no. 4 (2001): 046104.

Parameters

hurst (float) – a callable with one argument $h(t)$ such that $h(t') \in (0, 1) \forall t' \in [0, t]$. Default is $h(t) = 0.5$.
t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

property hurst¶: Hurst function.

sample ( n ) [source]¶

Generate a realization.

Parameters: n (int) – the number of increments to generate

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

class stochastic.processes.continuous. PoissonProcess ( rate=1, rng=None ) [source]¶

Poisson process.

A Poisson process with rate $\lambda$ is a count of occurrences of i.i.d. exponential random variables with mean $1/\lambda$. This class generates samples of times for which cumulative exponential random variables occur.

Parameters

rate (float) – the parameter $\lambda$ which defines the rate of occurrences of the process
rng (numpy.random.Generator) – a custom random number generator

property rate¶: Rate parameter.

sample ( n=None, length=None ) [source]¶

Generate a realization.

Exactly one of n and length must be provided.

Parameters

n (int) – the number of arrivals to simulate
length (int) – the length of time to simulate; will generate arrivals until length is met or exceeded.

class stochastic.processes.continuous. SquaredBesselProcess ( dim=1, t=1, rng=None ) [source]¶

Squared Bessel process.

The square of a Bessel process: $\|\mathbf{W}_t\|^2$.

The Bessel process is the Euclidean norm of an $n$-dimensional Wiener process, e.g. $\|\mathbf{W}_t\|$

Parameters

dim (int) – the number of underlying independent Brownian motions to use
t (float) – the right hand endpoint of the time interval $[0,t]$ for the process

property dim¶: Dimensions, or independent Brownian motions.

sample ( n ) [source]¶

Generate a realization.

Parameters: n (int) – the number of increments to generate

sample_at ( times ) [source]¶

Generate a realization using specified times.

Parameters: times – a vector of increasing time values at which to generate the realization

property t¶: End time of the process.

class stochastic.processes.continuous. VarianceGammaProcess ( drift=0, variance=1, scale=1, t=1, rng=None ) [source]¶

Variance Gamma process.

A variance gamma process has independent increments which follow the variance-gamma distribution. It can be represented as a Brownian motion with drift subordinated by a Gamma process:

\[\theta \Gamma(t; 1, \nu) + \sigma W(\Gamma(t; 1, \nu))\]

Parameters

drift (float) – the drift parameter of the Brownian motion, or $\theta$ above
variance (float) – the variance parameter of the Gamma subordinator, or $\nu$ above
scale (float) – the scale parameter of the Brownian motion, or $\sigma$ above
t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

property drift¶: Drift parameter.

sample ( n ) [source]¶

Generate a realization.

Parameters: n (int) – the number of increments to generate

sample_at ( times ) [source]¶

Generate a realization using specified times.

Parameters: times – a vector of increasing time values at which to generate the realization

property scale¶: Scale parameter.

property t¶: End time of the process.

property variance¶: Variance parameter.

class stochastic.processes.continuous. WienerProcess ( t=1, rng=None ) [source]¶

Wiener process, or standard Brownian motion.

Parameters

t (float) – the right hand endpoint of the time interval $[0,t]$ for the process
rng (numpy.random.Generator) – a custom random number generator

sample ( n )¶

Generate a realization.

Parameters: n (int) – the number of increments to generate

sample_at ( times )¶

Generate a realization using specified times.

Parameters: times – a vector of increasing time values at which to generate the realization

property t¶: End time of the process.

times ( n )¶

Generate times associated with n increments on [0, t].

Parameters: n (int) – the number of increments

andersonmookedis.blogspot.com

Source: https://stochastic.readthedocs.io/en/stable/continuous.html

How to Estimation Continuous Time Stochastic Processes

Continuous-time Processes¶

0 Response to "How to Estimation Continuous Time Stochastic Processes"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel